El "módulo flotante" de los Casio GM-B2100

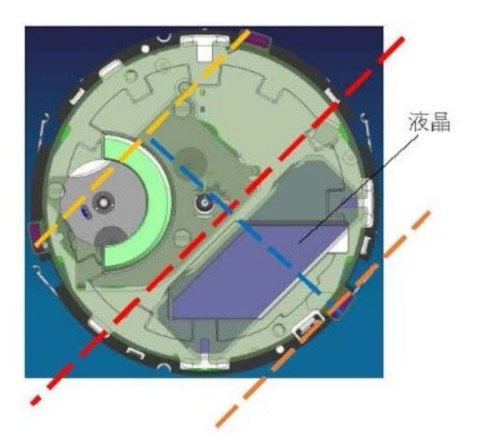
En el vídeo vemos una simulación en 3D de la deformación que ocurre en un 2100 convencional cuando sufre una fuerza frontal, en este caso pensemos que el reloj cae al suelo desde una altura X y aterriza justo sobre su cara frontal (sobre el cristal). En este caso (y en todos, claro) lo que primero que choca contra el suelo es el bisel y queda completamente frenado. El módulo sigue "cayendo" y topa contra el soporte interior que lo separa del cristal, que en este caso es un anillo que perimetra todo el dial del módulo, de forma que dicho anillo "frena" a su vez el módulo.

El módulo queda así frenado por sus laterales que a su vez deberían frenar todo el conjunto, pero, claro, los materiales (como todos) tienen una cierta elasticidad y el módulo empieza a deformarse.




¿Dónde concentra más masa un módulo que alberga un motor y un conjunto de engranajes central? Exacto, en el centro, así que ese peso en el centro de un módulo "flexible" hace que el anillo frene el modulo por los bordes al tiempo que el centro sigue avanzando hacia delante produciéndose así una deformación central de la pieza que llegará a provocar una rotura de aquellas partes que son menos elásticas, en este caso de los cristales de los displays, según comenta el artículo.

Eso se ve muy bien en el vídeo, que simula esa fuerza frontal producto de la caida en el momento del primer choque contra el suelo: el bisel tiene una cierta deformación elástica (está pensado para eso, que una deformación elástica es lo que te receta el medico para absorber energia en caso de choque) y el módulo al quedar frenado por los bordes de ese anillo sufre una deformación central que proyecta dicho centro hacia delante (los resultados de dicha deformación son 10 veces mayores a los reales en la imagen para que se vea mejor). Esto nos muestra lo que ocurre cuando se cae el reloj convencional GA-2100 con caja de resina.

Pero los GM-B2100 de caja de acero son muy diferentes, precisamente por el material que utilizan.



¿Y qué pasa con el acero?, pues que:

A) necesita mucha más energía para deformarse (traducción: en estos parámetros en los que nos movemos, se comportará prácticamente como un cuerpo inelástico, es decir que no se deformará ni absorberá energía del choque como vemos que sí ocurre en cierta medida en el vídeo con un bisel elastomérico de resina blandita).

B) que pesa. Pesa mucho. Pesa muchísimo más que la resina y por ello ese conjunto de bisel-caja-módulo pesará mucho más y, si dobla su masa, sabiendo que la energía cinética del golpe es 1/2 de la masa por la velocidad al cuadrado y esa masa se dobla (que no la dobla, seguro que la multiplica por más de dos y de tres), pues la energía del impacto también es el doble (o el triple, o el cuádruple o lo que sea; sólo hay que comparar el peso del conjunto de la version de bisel metálico con la de resina y ése es el factor por el que hay que multiplicar la energía del golpe en el modelo de resina para saber cuántas veces mayor es la energía del golpe en el modelo de metal del GMB 2100, respecto al modelo en resina GA-2100.

En resumen, que cuando teníamos el modelo original de resina, éste se caía de diez metros y no se despeinaba nadie, y ahora con la versión de metal se nos cruje el display!

¿Creéis que los ingenieros de Casio se quedaron tranquilos viendo esto? Claro que no, así que había que apretarse los cáncamos y ponerse a pensar y tiraron por las simulaciones éstas tan hermosas que nos han deleitado en la animación.

Pues eso, que los ingenieros vieron que si en el aterrizaje se frena uniformemente todo el reborde del módulo con una estructura contínua como un anillo, la parte central deforma el conjunto y hace catacrac el display.

Y ahí es donde salen los otros dibujitos (éstos 2D pero con colorines) que vamos a poner y explicar ahora mismo.





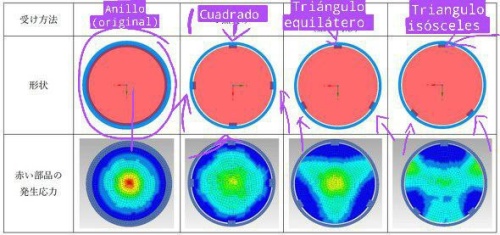
Me he limitado a anotar la terminología que emplea el artículo en la parte superior y a señalar con unas flechitas dónde está cada apoyo en cada "prototipo" que se ha probado (no empleo la palabra "modelo" para no confundir con los relojes).

El primero de izquierda a derecha ("anillo original ") es el anillo como el que monta el GA-2100 de resina y que bastaba para proteger su módulo frente a la energía que generaba su escasa masa en una caída de 10 metros, como marcan los cánones de todos los G-Shock.

Se ve por los colores que los bordes quedan frenados y no flexan (azul oscuro), pero a medida que nos acercamos al centro vemos que el color va cambiando de menor a mayor deformación (o energía, o concentración de lineas de fuerza, que a efectos prácticos son medidas equivalentes para este caso), alcanzando un valor muy alto en el centro como veíamos en la simulación 3D del inicio.



En la segunda imagen ("cuadrado") se emplean ya cuatro puntos de apoyo en vez de todo el anillo. Como veis, la cosa cambia mucho en cuanto a deformación (vamos a pensar que los cambios de color obedecen a una escala lineal) y en el centro se genera mucha menos deformación. Vamos bien, pero aún hay mucho estrés en zonas próximas a las delicadas estructuras de cristal de los displays y puede que con esta mejora no bastara para que éstos sobrevivieran al aumento tan grande de energía del choque con el GMB-2100 con su bisel de metal respecto al GA-2100 de resina.

En el tercer dibujito ("triangulo equilátero") vemos algo similar pero con tres puntos de apoyo en vez de cuatro. Como vemos, igual que en el caso anterior, la deformación de los bordes ayuda a que se difunda la energía y que no se concentre tanto en el centro con la consecuente deformación que ya veíamos que no queremos tener (hay que recordar que la energía total, es decir la suma de todas estas energías generadas en el módulo en la caida, siempre será la misma en todos los casos; sólo buscamos que se reparta de una manera determinada para no dañar los componentes). Pero tampoco supone una mejora tan grande respecto a la del cuadrado ya que hay una deformación bastante simétrica y el centro sigue concentrando mucha energía.



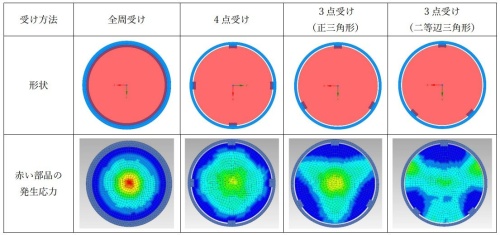
En la cuarta figura ("triangulo isósceles") vemos ya un "state of art", es decir que hemos visto cómo las fuerzas de deformación se van anulando unas con las otras (o mejor dicho, cómo una deformación va compensando la otra en cierta manera y transfiriéndose dichas deformaciones hacia otras partes) tanto en el modelo del cuadrado como en el del triángulo equilátero. Y aquí nos preguntamos qué pasaría si redirigimos parte de esa energía (o esa deformación consecuente) a zonas donde no hay peligro de que se rompa nada.

Y ¡bingo!, vemos que separando estudiadamente los puntos de apoyo (ahí un software de este tipo es donde saca su valor, ahorrándote mucho trabajo de cálculo y pruebas) alcanzamos un resultado donde el centro se deforma mucho menos (o se reparte mucho más en toda la superficie, que pensándolo así parece más fácil de verse el resultado) y entre los dos vértices de la base del triángulo se deforma aún menos, lo cual es justo lo que buscábamos para proteger esas frágiles pantallitas que tanto trabajo nos han dado.



Si os ha sonado un poco raro al principio aunque ahora lo veáis más lógico, no os preocupéis que ya nos dicen los propios ingenieros que hicieron el estudio que tuvieron que convencer a los demás de que los resultados eran correctos, porque parecía algo muy contraintuituvo que esa solución basada en sólo tres puntos de apoyo protegiera mejor los displays que una que distribuyera la energía por en más puntos del módulo, aunque el último paso, el cambio de triángulo equilátero a isosceles (o acercar dos puntos de los tres a la zona que no se quiere que se deforme), una vez asimilada la lógica de la deformación que producía la rotura, ya sea un poco mas fácil de entender al final.

Y con esto ya hemos dado una primera aproximación al estudio de la distribución de fuerzas en un choque. Cómo veis la propia elasticidad de los elementos que queremos proteger a veces puede jugar en nuestra contra pero con un adecuado estudio detrás podemos invertir las tornas.

Valorémoslo adecuadamente cuando nos pongamos el cinturón de seguridad, el casco de la bici o el G-Shock de varios cientos de euros/dólares, que estas cosas no se estudian solas y cuestan pasta.


| Redacción: Cockey en Telegram ZonaCasio | Gracias a Alberto